Ergänzungen, Fragen und Antworten:

Prüfquotientenbildung

Auf Anregung von ELMAR SCHMIDT wird die Bildung und Bewertung der Prüfquotienten noch etwas detaillierter beschrieben. Diese Ergänzung (zur 1.; 2. Auflage) wird für eine zukünftige 3. Auflage vorgesehen und kann hier vorab als *.pdf Dokument herunter geladen werden.

Aus dieser Anregung stammt auch ein weiteres Rechenbeispiel zur Maximum-Optimierung (als *.pdf-Datei) mit mehrfachen Prüfquotientenbildungen.

Zweite Zielfunktion

Auf Anregung von PAUL SOLTERMANN wird die Bildung und Bewertung der zweiten Zielfunktion abgeändert. Diese Ergänzung (zur 1.; 2. Auflage) wird für eine zukünftige 3. Auflage vorgesehen und kann hier vorab als *.pdf Dokument herunter geladen werden.

Aus einem Mischungsproblem für Viehfutter, in dem eine Maximierung eines Nährstoffes gefordert ist, ergab sich ein Fehler im Algorithmus, der bisher nirgends in der Literatur beschrieben wurde...

Da zumeist Minimum-Probleme zu lösen sind oder in Maximum-Problemen ∀ x_i=0 zulässig sind, wurde dieses Problem bisher nicht bemerkt und folglich nicht beschrieben. Das Problem tritt also in Maximum-Problemen mit Einschränkungen nach unten auf.

2.3.1    Nachschub-Problem

SILVIA HUMBERG fragt nach, ob das Nachschubproblem (Abschnitt 2.3.1) auch auf nichtleere Lösungen gezwungen werden kann, für den Fall 'zu großer Bestellmengen', also für den Fall, dass größere Mengen bestellt werden, als geliefert werden können.

Antwort: Im Allgemeinen ist es sicher nicht sinnvoll, davon auszugehen, dass etwas nicht Vorhandenes geliefert werden kann. Eine Bestellannahme unter der Voraussetzung der Nichtlieferbarkeit kann sicher nur erfolgen, falls die Ware anderweitig beschafft werden kann, oder verspätet – nach einer entsprechenden späteren Produktion geliefert werden darf...

Nicht überzeugt von der Richtigkeit eines solchen unternehmerischen Handelns des '(Waren-) Konto überziehens', werden hier zwei Lösungsmöglichkeiten angeboten:

Version 1:

Es wird die Nichtnegativität des Lagerbestandes ignoriert. Die Gleichungen des Abschnitts 2.3.1.5 entfallen einfach. Dann kann auch (in der Beschreibung) Ware geliefert werden, die nicht vorhanden ist. Wie eine solche Lieferung dann tatsächlich erfolgen kann, bleibt dabei natürlich offen!

Diese Sicht ist, es sei noch einmal betont, unrealistisch und der Sinn der Lagerhaltung als Puffer zwischen der Produktion und der Abnahme wird nicht erfüllt.

Version 2:

Es wird eine 'Kontoüberziehung' durch die Warenlieferung mittels Dritter (etwa eine Warenbeschaffung über Konkurrenten) oder mit Verzug, durch Nachproduktion, zu entsprechend größeren Kosten angenommen.

Dieses lässt sich mittels der Hinzufügung virtueller Produzenten beschreiben. Dabei wird einem jeden realen Produzenten ein virtueller Produzent zugeordnet, der die gleichen Lager beliefern kann, wie der reale Produzent. Der virtuelle Produzent wird ohne Produktionsbeschränkung beschrieben (Abschnitt 2.3.1.4), seine Lieferkosten werden jedoch extrem groß angesetzt. Die Lieferkosten sollten jedenfalls stets größer sein, als die realen Lieferkosten aller Produzenten an die Lager sowie die Lieferkosten der Lager unter einander. Gegebenenfalls können natürlich die bekannten Kosten für die Beschaffung über Dritte angesetzt werden.

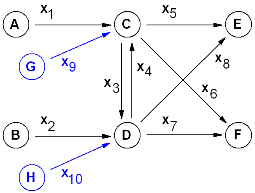
Im Beispiel B 2.3.1 könnten etwa die virtuellen Produzenten G, H eingeführt werden und die Liefermengen mit x₉, x₁₀ zusätzlich eingeführt werden. Da die Kosten der Lieferungen zu den Lagern und zwischen den Lagern bisher nicht größer als 50 Taler/1 waren, werden nun die virtuellen Lieferkosten zu den realen Lagern mit 100 Taler/1 angenommen. Damit sind die virtuellen Lieferungen für real mögliche Bestellmengen stets Null.

2.3.3    Kleeblatt-Problem

WOLFGANG REH fragt, wie ein Kleeblatt-Problem zu lösen ist, falls die Transportkapazität der einzusetzenden Fahrzeuge kleiner als die Gesamttransportmenge ist (dieses führe auf eine leere Lösung).

Antwort: Die Fahrzeuge des Kleeblatt-Problems müssen nicht physisch existent sein, sie dürfen auch virtuell sein. Können Fahrzeuge mehrfach (zeitlich nach einander) eingesetzt werden, werden virtuelle Fahrzeuge ausreichender Anzahl definiert. Sofern nicht weitere Einschränkungen bezüglich der maximalen Anzahl der Einsatzfahrten bestehen, wird die Anzahl der virtuellen Fahrzeuge gleich dem -- zur ganzen Zahl aufgerundeten -- Quotienten aus der Gesamttransportmenge m_ges und der Transportkapazität m_Fahrzeug des jeweiligen Farzeuges gesetzt.

Die Anzahl n_Fahrzeug der virtuellen Fahrzeuge eines physischen Fahrzeuges wird damit zu
n_Fahrzeug = -int( -m_ges / m_Fahrzeug )

Beispiel: Ein Fahrzeug A habe die Transportkapazität m_A = 10 und ein zweites Fahrzeug B habe die Transportkapazität m_B = 12.
Ein Transportauftrag erfordere die Transportmenge m_ges = 35.

Vom Fahrzeug A wird dann die Anzahl n_A = -int( -35 / 10 )
n_A = 4 Fahrzeuge benötigt

Vom Fahrzeug B wird dann die Anzahl n_A = -int( -35 / 12 )
n_A = 3 Fahrzeuge benötigt

Es werden daher die Fahrzeuge A_1; A_2; A_3; A_4; B_1; B_2; B_3 definiert.